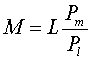10. L' immersione a quote più elevate di quella del mare.

Anche se non tutti le praticano, le immersioni nelle acque di montagna non sono una rarità nel vasto panorama della subacquea. Rispetto alle immersioni effettuate in mare, esse presentano tuttavia alcune importanti differenze che si devono considerare sia nella fase di pianificazione sia in quella di esecuzione.

10.1 Le caratteristiche delle acque di montagna.

Le caratteristiche delle acque di montagna che hanno maggiore rilevanza ai fini della sicurezza sono quattro:

·      la temperatura dell' acqua è generalmente più bassa di quella del mare; anche nei mesi più caldi essa raramente supera il valore di 10-12 °C e, spesso, neppure li raggiunge;

·      la spinta di galleggiamento è inferiore. Infatti la concentrazione di sali in acqua dolce è molto più bassa di quella che si trova in mare (se non praticamente nulla) e la densità è minore, con la conseguenza che  anche l' effetto del principio di Archimede è minore;

·      dato che la quota è più elevata di quella del mare, la pressione è sempre inferiore ad 1 Atm. (Per citare un valore significativo, a 5000 di altezza sul livello del mare la pressione è circa 0,5 Atm.);

·      negli specchi d' acqua dolce le correnti possono essere molto più imprevedibili che in mare.

10.2 L' attrezzatura.

La temperatura solitamente bassa delle acque di montagna richiede una attrezzatura in grado di proteggere il corpo dalla dispersione di calore molto più di quanto non sia necessario, in generale, nel caso delle immersioni in mare durante la bella stagione.

Lo spessore medio (5-6 mm.) delle normali mute di neoprene è quasi sempre insufficiente nelle acque montagna. Inoltre, il taglio ed il confezionamento delle mute tradizionali non garantiscono l’ impermeabilità necessaria quando l' acqua è decisamente fredda; in casi del genere la muta stagna o, almeno, quella semi-stagna diventano quasi irrinunciabili.

I dettagli relativi a questi due particolari componenti dell' attrezzatura saranno descritti nel prossimo capitolo, dedicato proprio alle immersioni in acqua fredda.

10.3 Il galleggiamento.

Come si è detto, l' acqua dolce è meno densa dell' acqua di mare e quindi fornisce una spinta di galleggiamento inferiore; in altre parole, a parità di equipaggiamento il corpo affonda di più nell' acqua dolce che in quella di mare, Questo significa che per le immersioni in acqua dolce sarà sufficiente una zavorra che pesi il 5-15%  meno di quella usata solitamente in mare.

10.4 I fenomeni legati alla pressione atmosferica.

La pressione atmosferica è il peso esercitato sulla superficie della terra dall' aria che la sovrasta. Ad esempio, il peso della colonna d' aria che grava su 1 cm² di superficie a livello del mare (la "colonna d' aria elementare") è circa 1,03 kg, si chiama Atmosfera (abbreviata con Atm. e detta anche Bar o Hectopascal, con poca differenza); si misura in Kg/cm²

Immaginiamo che questa colonna sia formata da tanti strati di aria sottilissimi, sovrapposti come foglietti carta. Sullo strato numero 1, che sta a contatto con la superficie della terra, grava il peso di tutti quelli che lo sovrastano; sul numero 2 grava il peso di tutti meno il peso del numero 1, che gli sta sotto; sul numero 3 grava il peso di tutti meno quello del numero 1 e del numero 2, e così di seguito. Sintetizzando, si osserva che il peso totale degli strati d' aria diminuisce mano a mano che diminuisce il loro spessore complessivo. Meno banalmente, si dice che la pressione atmosferica diminuisce con l' aumentare della quota.

10.5 I fenomeni legati alla densità dell' acqua.

La quantità dei sali minerali disciolti nei fiumi e nei laghi è irrilevante; in pratica, le densità ed il peso specifico di queste acque sono circa uguali a quelli dell' acqua distillata ed un litro pesa 1 Kg. Invece, la quantità di minerali disciolta nel mare è di circa 30 grammi per litro[1], quindi 1 litro d' acqua di mare pesa circa 1,03 Kg.

Dato che il volume di 1 litro equivale a 1000 cm³, se immaginiamo di sovrapporre uno sull' altro tutti questi 1000 cubetti otterremo una colonna alta 10 m. (detta "colonna d' acqua elementare"), che pesa 1,03 Kg. e grava sulla superficie di 1 cm²; in altre parole, questa colonna esercita la pressione idrostatica di 1,03 Kg/cm².

Questo valore è uguale alla pressione atmosferica al livello del mare; cioè  anche la pressione idrostatica di una colonna d' acqua elementare ha il valore di 1 Atm.

Analogamente alla pressione atmosferica, anche la pressione idrostatica varia secondo l' altezza (o, per meglio dire nel caso dell' acqua, secondo la profondità) ed aumenta mano a mano che lo strato d' acqua diventa più spesso. Infatti:

·      2 colonne d' acqua elementari sovrapposte esercitano la pressione di 2,06 Kg/cm² ossia: la pressione idrostatica di una colonna alta 20 metri è 2 Atm.),

·      3 colonne d' acqua elementari sovrapposte esercitano la pressione di 3,09 Kg/cm² (ossia : la pressione idrostatica di una colonna alta 30 metri è 3 Atm.),

e così via.

Sintetizzando, possiamo dire che la pressione atmosferica al livello del mare e la pressione idrostatica a 10 metri di profondità sono uguali e misurano entrambe 1 Atm.

Più precisamente, tenendo conto del diverso peso specifico dell' acqua di mare e di quella di lago o fiume, si ha che la pressione idrostatica:

·      è 1 Atm. a 10 metri ( e varia di 1 Atm. ogni 10 m.) nel mare;

·      è 1 Atm. a 10, 3 metri ( e varia di 1 Atm. ogni 10,3 m.) in acqua dolce.

10.6 Gli effetti.

Dato che la pressione atmosferica diminuisce con l' aumentare della quota, nelle stesse condizioni e nella stessa proporzione diminuisce anche la pressione parziale dell' azoto che dell' aria è componente all' 80%. circa. Quindi se al livello del mare la pressione atmosferica è 1 Atm., la pressione parziale dell' azoto è 0,8 Amosfere.

Se ad una quota di montagna la pressione atmosferica è, per esempio, 0,9 Atm. anche la pressione parziale dell' azoto si riduce pur conservando il suo rapporto pari all' 80%; dato che l' 80% di  0,9 è 0,76, questa sarà appunto la pressione parziale del' azoto nel nostro esempio. 

Da questo si deduce che mentre al livello del mare il rapporto fra pressione atmosferica e pressione idrostatica è 1:1 (entrambe valgono 1 Atm.), man mano che si sale in quota questo rapporto diminuisce progressivamente.

Infatti la pressione idrostatica rimane sempre costante (perché il peso dell' acqua non varia) mentre la pressione atmosferica decresce progressivamente (perché la colonna d'aria diventa sempre meno pesante). E se questo vale per la pressione atmosferica, vale anche per la pressione parziale dell' azoto che della pressione atmosferica rappresenta l' 80%.

Tutto questo per dire che, nel caso di immersioni in acque di montagna l' assunzione e l' eliminazione dell' azoto hanno un andamento differente da quello relativo alle immersioni in mare e questa differenza dipende dalla diversa pressione atmosferica. Ovviamente, ciò si riflette anche sui parametri della decompressione.

In particolare, a parità di permanenza in acqua, l' azoto accumulato durante l' immersione in un lago di montagna ad una certa profondità equivale all' azoto assunto durante una immersione in mare ad una profondità maggiore. Per avere una idea più precisa si applica la seguente formula:

;

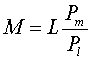nella quale :

·      M è la profondità equivalente[2] nel mare;

·      L è la profondità raggiunta nel lago;

·       è la pressione a livello del mare (pari ad 1 Atm.);

·       è la pressione atmosferica sulla superficie del lago.

Per esempio, se ci immergiamo a 19 metri in un lago elevato 2000 m. sul livello del mare su cui agisce la pressione atmosferica di circa 0,8 Atm., applicando la formula si avrà:

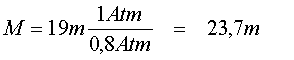
Ossia, a 19 metri di profondità nel lago l' organismo assume la stessa quantità di azoto che in mare assumere a circa 24 metri.

Analogamente, cambiano anche le quote per la decompressione; cioè, la quantità di azoto che in mare si elimina - per esempio - durante la sosta a 5 metri, nel lago si elimina ad una profondità diversa. Il calcolo si fa con la stessa formula, nella quale:

 indica la profondità, ricavata dalle tabelle, a cui si effettua la sosta di decompressione in mare;

 indica la profondità, da calcolare, a cui la sosta di decompressione deve essere invece effettuata nel lago;

  è la pressione a livello del mare (1 Atm.);

  è la pressione atmosferica sulla superficie del lago.

Nel caso del nostro esempio, la formula  diventa quindi:

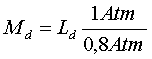
Se le tabelle prescrivono una sosta a 5 metri in mare, si avrà :

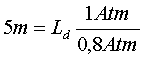
ossia :

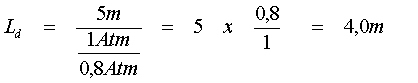
che si legge così: se una certa immersione in mare rende necessaria una sosta di decompressione a 5 metri, lo stesso profilo d’ immersione in un lago elevato 2000 metri sul livello del mare richiede la decompressione a 4 metri.

E' quindi evidente che i valori di profondità delle tabelle "marine" non possono essere presi così come sono anche per le immersioni in alta quota ma devono essere ricalcolati.

La fatica di questi calcoli, assieme al rischio di commettere errori di calcolo, può essere evitata usando le tabelle specificamente costruite per le immersioni in quota. Esse, pur non essendo diffuse come quelle marine, sono comunque disponibili in commercio.

Per contro, quasi tutti i computers da immersione sono adatti anche alle acque di montagna, almeno fino ad una certa elevazione sul livello del mare[3]. Infatti essi sono in grado di rilevare la pressione ambiente e di adeguarvisi automaticamente (anche se è questa è sensibilmente diversa da quella al livello del mare), elaborano correttamente i vari dati e forniscono indicazioni conseguentemente appropriate e sicure.